Lecciones Preliminares de Lógica VII
VII. Lógica predicativa de primer orden
Rudīmenta Artis Quaerendī VII
Parte de:
Lecciones Preliminares de Lógica
(Lógica para el estudio de Metafísica)
Por Ālyssa Nova (Ἀλύσσα Καινούργια)
ADEPTVRIS DOCTRINAM ***
ARS QVAERENDĪ ***
Tabla de contenidos
Lógica predicativa de primer orden
Rudīmenta Artis Quaerendī VII
Parte I
En la sección anterior analizamos algunas formas válidas de inferencia en la lógica proposicional. Partiendo de los cimientos de la lógica proposicional, los lógicos han construido lógicas más poderosas, lógicas que reconocen un mayor número formas de argumentación válidas que la lógica proposicional por sí sola. Estas lógicas profundizan en la estructura de nuestras afirmaciones y serán indispensables para representar las opiniones y los argumentos que encontramos en la metafísica contemporánea.

En la presente lección, analizaremos la lógica predicativa de primer orden —o simplemente: lógica predicativa, lógica de primer orden, o lógica de predicados—, desarrollada inicialmente por Gottlob Frege (veremos más adelante el por qué de esta denominación de lógica de primer orden). Esto nos proporcionará algunas herramientas que nos serán útiles en futuros análisis y discusiones de cuestiones relativas a la ontología.1Recordemos que estamos ante unas lecciones preliminares que son propedéutica a un curso introductorio a la metafísica. Pero, comencemos por algo simple. Consideremos el siguiente argumento:
Argumento 6
1. Miguel respeta a todos los que aman a los Beatles.
2. Laura ama a los Beatles.
Por lo tanto,
3. Miguel respeta a Laura.
No podemos demostrar la validez de este argumento empleando unicamente las herramientas de la lógica proposicional de la sección anterior. No nos resultaría visible, si lo planteamos de la siguiente forma:
1. A
2. B
Por lo tanto,
3. C
Pero esta no es una forma válida de argumento. Nos veríamos obligados a simbolizarlo de esta manera porque cada proposición (1), (2) y (3) es distinta y ninguna contiene el tipo de partes que nos permitirían usar los conectivos introducidos en la sección anterior.
Pero el argumento anterior es intuitivamente válido, y por lo tanto, para demostrarlo usando lógica simbólica, necesitamos más herramientas con las que simbolizar el argumento.2Claro está que podríamos utilizar el método que aprendimos en la lección sobre Validez. La lógica predicativa de primer orden nos proporciona las herramientas pertinentes. La idea principal es reconocer que, en general, podemos separar las proposiciones en sujetos (o grupos nominales) y predicados.
Para tomar un caso simple, considere el enunciado:
Marco es ordenado.
En la lógica de predicados, el símbolo para un predicado («es ordenado») es siempre una letra mayúscula. En este caso, usaremos «O». El símbolo para el predicado se coloca antes del símbolo para el sujeto («Marco»). Usaremos «m» para representar a «Marco». El enunciado o proposición completa se simbolizará entonces en la lógica de predicados de la siguiente manera:
Om.
De manera similar, «Robert es un filósofo» podría simbolizarse como:
Fr.
También podríamos querer simbolizar el enunciado:
Marco admira a Robert.
Esto sería:
Amr.
Observemos con atención que el símbolo del predicado (en este caso, «admira») siempre va al frente. Aquí nuestro predicado, «admira», es un predicado de dos posiciones porque toma dos grupos nominales como entradas.3A diferencia de «Marco es ordenado» y «Robert es un filósofo», en los que nos encontramos frente a predicados de una posición. Pero, por supuesto, existen predicados que toman más de dos entradas. Por ejemplo, si ha jugado al Cluedo —o al Clue, si vive en América—, probablemente haya formulado enunciados usando predicados como:
____ asesinó a ___ en el/la ___ usando el/la ___

Por ejemplo, podríamos decir:
El profesor Mora asesinó al señor Blanco en la terraza usando el candelabro.
Esto se puede representar como:
Ambtc.
Algo que será especialmente importante en nuestros primeros encuentros con nociones de metafísica es que podemos representar enunciados que hagan referencia a alguna(s) persona(s) u objeto(s), pero sin usar un nombre. Enunciados tales como:
- Alguien es ordenado.
- Alguien asesinó al Sr. Blanco en la terraza usando el candelabro.
O, también:
- Nadie es ordenado.
- No hay nada con lo que el Profesor Mora haya asesinado al Sr. Blanco en la terraza.

Para representar enunciados como estos, la lógica predicativa de primer orden utiliza variables (símbolos como x, y, z, etc.) y lo que se llama cuantificador existencial. El cuantificador existencial se representa utilizando: ∃. Por ejemplo, considere el enunciado:
Alguien es ordenado.
Este se simbolizará como:
∃xOx.
Esto se puede leer en voz alta de cualquiera de las siguientes maneras:
- Existe una x tal que x es ordenado.
- Existe al menos una x tal que x es ordenado.
- Alguna x es ordenada.
- Algo es ordenado.
Si sabemos que nuestro dominio de cuantificación incluye solo personas (aprenderemos más sobre el dominio de cuantificación en un momento), podemos leer esto como:
- Alguien es ordenado.
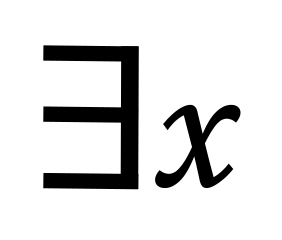
También podemos usar una variable y un cuantificador existencial para traducir el enunciado «Alguien asesinó al Sr. Blanco en la terraza usando el candelabro», como:
∃xAxbtc.
Podemos leer esto como: «Existe una x tal que x asesinó al Sr. Blanco en la terraza con el candelabro».
También podemos representar el enunciado: «Hay algo con lo que el Profesor Mora asesinó al Sr. Blanco en la terraza, como:
∃xAmbtx.
Repare en que la variable «x» reemplaza el nombre del objeto sobre el que estamos cuantificando, es decir, el referente de la frase cuantificadora «algo» o «alguien». En el primer caso, «alguien» se refiere a la «x», que es el asesino, por lo que la variable va en primer lugar. En la segunda oración, «algo» se refiere a la «x», que es el arma homicida, por lo que la variable va en último lugar.
También podemos representar enunciados más complejos utilizando el cuantificador existencial. Por ejemplo, podemos simbolizar «Nada es ordenado» como:
¬∃xOx.
Para decir que hay algo que es ordenado y amigable, podemos utilizar la siguiente traducción:
∃x (Ox ∧ Ax),
donde «Ox» significa que «x» es ordenado y «Ax» significa que «x» es amigable.
O bien, expresar:
Hay al menos un águila bebé en esa montaña.
Puede simbolizarse como:
∃x ((Bx ∧ Ax) ∧ Mx).
Finalmente, en algunos casos, nos encontraremos con enunciados que necesitan más de una variable de cuantificación. Por ejemplo, uno podría querer expresar en lógica de predicados el enunciado:
Algunos gatos aman a algunos perros.
Este enunciado tiene dos frases cuantificadoras. Esta frase expresa tanto que existe una «x» tal que «x» es un gato, pero también expresa que existe una «y» tal que «y» es un perro, y que el gato (la «x») ama al perro (la «x»). Para no confundir qué variable se refiere al gato y cuál al perro, usaremos variables distintas «x» e «y» en la simbolización de este enunciado:
∃x∃y ((Gx ∧ Py) ∧ Axy),
que podemos leer en español como «Existe una ‘x’ y existe una ‘y’ tal que ‘x’ es un gato e ‘y’ es un perro, y la ‘x’ ama a la ‘y’».
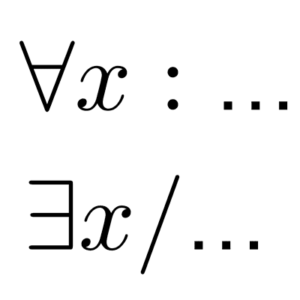
Nótese que en todos los casos donde se usa una variable (x, y, z, etc.) como parte de un enunciado completo, la variable siempre debe estar contenida dentro del alcance de un cuantificador (“the scope of a quantifier” en inglés). Este alcance, o bien está justo al lado del cuantificador en el enunciado, o debe haber un rango entre paréntesis que se extienda desde un cuantificador y que incluya la ocurrencia de esa variable. Considere las variables en los siguientes dos enunciados.
Fx
∃xFx ∧ Gx
En el primer enunciado, «x» no está contenida dentro del alcance de ningún cuantificador, y por lo tanto este enunciado no expresa un pensamiento completo. Dice «x es F», donde «x» no tiene ningún significado claro. En el segundo caso, la «x» en la frase «Gx» no está contenida dentro del alcance de ningún cuantificador, y por lo tanto, nuevamente, la referencia de esta «x» no está clara. ¿Se supone que esta «x» que es G es la misma que la «x» que es F? Esto no está claro. Para solucionar esto, podemos introducir paréntesis:
∃x (Fx ∧ Gx).

Ahora todas las variables en la oración se encuentran dentro del alcance del cuantificador «∃» y podemos entender que este enunciado dice: «Existe algo que es tanto F como G». Cuando decimos que una variable se encuentra dentro del alcance de un cuantificador, estamos diciendo que es una variable ligada.4En inglés: bound variable. Al simbolizar enunciados completos en lógica predicativa, es importante que todas las variables estén limitadas por cuantificadores, ligadas a ellos.

En general, cuando uno hace una afirmación cuantificada existencialmente, está diciendo que existe algo que es de cierta manera. El tipo de cosa que tenemos en mente generalmente depende del contexto. Como lo expresan los lógicos, esto depende del dominio de cuantificación,5En inglés: Domain of quantification. el conjunto de entidades sobre el que se extienden los cuantificadores. Por ejemplo, supongamos que usamos «Bx» para simbolizar «x es bendecido», y luego vemos el enunciado:
∃xBx.
Lo que este enunciado supuestamente representa depende del dominio relevante de cuantificación. El dominio de cuantificación puede ser:
- el conjunto de todas las entidades que existen, de modo que la oración puede leerse como: «Algo es bendecido»,
- el conjunto de personas que existen, de modo que la oración puede leerse como: «Alguien es bendecido»,
- el conjunto de personas en una comunidad particular en discusión, por ejemplo, aquellos en esta casa. Entonces, «∃xBx» significaría: «Alguien en esta casa es bendecido».
El dominio relevante de cuantificación está determinado por el contexto. En nuestra incursión a la metafísica veremos a los filósofos hacer referencia a este hecho. Al expresar sus teorías, explotarán explícitamente el hecho de que nuestros cuantificadores a veces pueden estar restringidos, de modo que abarcan un conjunto limitado de objetos. O en otras ocasiones, un filósofo aprovechará el hecho de que en algunos casos nuestros cuantificadores pueden ser «completamente abiertos», lo que significa que abarcan el dominio de cuantificación más grande posible, incluyendo cualquier entidad.
Estamos ahora en posición de poder distinguir tres tipos de símbolos alfabéticos que se utilizan en la lógica predicativa de primer orden.
Pero —permítasenos la digresión—, estamos también en posición de explicar el por qué del nombre de esta lógica: lógica de primer orden. En el tipo de lógica de predicados que estamos discutiendo aquí, las variables se utilizan para abarcar entidades (personas, gatos, perros, teléfonos móviles, etc.). Pueden usarse para reemplazar nombres, como cuando pasamos de «Om» (Marco es ordenado) a «∃x Ox» (Alguien es ordenado). En la lógica de segundo orden, las variables también se introducen para representar propiedades o atributos, las formas en que son las entidades. Luego entonces, pueden reemplazar predicados, por ejemplo, si quisiéramos pasar de «Om» (Marco es ordenado) a «∃F Fm» (Marco es de alguna manera). El estatus de la lógica de segundo orden es controvertido. Y esta controversia está directamente relacionada con la cuestión metafísica sobre el estatus de entidades abstractas como propiedades o atributos. Analizaremos este debate más a fondo cuando hablemos de «entidades abstractas» en lo referente a metafísica contemporánea.6Que desafortunadamente aún no trataremos en estas lecciones preliminares de lógica. Contacte con nosotros para considerar su incorporación al Atrium Philosophicum. Show the love! Por ahora, simplemente continuaremos usando la lógica de primer orden.
Volvamos, pues, a nuestra lógica de primer orden y a la distinción de tres tipos de símbolos alfabéticos:
- Predicados, que se simbolizan con letras mayúsculas: F, G, H,…
- Nombres, que se simbolizan con letras minúsculas del principio del alfabeto: a, b, c,…
- Variables, que se simbolizan con letras minúsculas del final del alfabeto: x, y, z, w, u, v,…
Además del cuantificador existencial, existe también otro cuantificador, el cuantificador universal, que se utiliza para simbolizar afirmaciones que implican «todo» o «todos». Por ejemplo:
Todos son bienaventurados,
puede simbolizarse como:
∀xBx.
Podemos leer esto como:
- Para todo ‘x’, ‘x’ es bienaventurado.
- Toda ‘x’ es bienaventurada.
- Todo el mundo es bienaventurado.
(Tenga en cuenta que si los únicos tipos de entidades que normalmente consideramos que tienen estados emocionales como la bienaventuranza son las personas, el dominio relevante de cuantificación es el conjunto de todas las personas).
Para tomar otro ejemplo, «Todos son filósofos bienaventurados», puede traducirse como:7emplearemos P de philosophī.
∀x (Bx ∧ Px)
Interpretado como: toda «x» es tal que es bienaventurado y filósofo.
¿Cómo simbolizaríamos «Todos los filósofos son bienaventurados»? Esto expresa algo diferente a decir que todo el mundo, sea quien sea, es feliz y filósofo (∀x(Bx ∧ Px)). «Todos los filósofos son felices» se simboliza utilizando el símbolo «⊃» que expresa: «si… entonces»:
∀x (Px ⊃ Bx).

Podemos leer esto en castellano lógico como «Para toda ‘x’, si ‘x’ es un filósofo, entonces ‘x’ es bienaventurado». Esto dice lo mismo que nuestro original «Todos los filósofos son bienaventurados», que por supuesto es diferente a decir «Algunos filósofos son bienaventurados», que se expresa en lógica de primer orden como:
∃x (Px ∧ Bx),
Es decir, «Existe una ‘x’ tal que ‘x’ es un filósofo y ‘x’ es bienaventurado».
¡Excelente considérese ya parte del grupo de ‘x’, en ‘Bx’. Ahora, antes de continuar a la Parte II, le conminamos a resolver el Ejercicio 8.
Parte II
En futuras aproximaciones a la metafísica contemporánea veremos que la formulación de tesis y argumentos en el lenguaje de la lógica de predicados de primer orden es a menudo esencial. En particular, cuando consideramos cuestiones de existencia, tendremos que formular y/o leer enunciados en lógica predicativa. Sólo entonces podremos tener claro lo que se sigue de ellos. Para ello, necesitaremos tener en nuestro haber algunas reglas básicas de inferencia que impliquen enunciados cuantificados existencial y universalmente.
Hay cuatro reglas básicas que se resumen en la Tabla 3. Algunas de estas reglas son un poco complicadas, pero para nuestros propósitos en este y próximas lecciones, las reglas que se utilizarán con más frecuencia son la Introducción del Cuantificador Existencial (IE) y la Generalización del Cuantificador Universal (GU). Así que consideremos brevemente algunos ejemplos que utilizan estas reglas de inferencia.
Veamos un ejemplo del tipo de inferencia que emplearemos cuando tratemos el tema de las «entidades abstractas». Supongamos que alguien cree lo siguiente:
La humildad es una virtud.
Esto se simbolizará en la lógica predicativa de primer orden como:
Vh.
Utilizando la regla IE, podemos concluir:
∃xVx.
Esto puede leerse como: «Existe algún ‘x’ tal que ‘x’ es una virtud».
Para considerar otro ejemplo, supongamos que tenemos razones para creer lo siguiente:
Platón es un filósofo que enseñó a Aristóteles.
Podemos simbolizar esto como:
Pp ∧ Epa (Platón es un filósofo8Philosophus y Platón enseñó a Aristóteles.)
Y luego utilizando IE, podemos inferir:
∃x(Px ∧ Exa).
En ambos casos de aplicación de IE, lo que estamos haciendo es introducir una variable ‘x’ para que sustituya a un sujeto en particular.
Observemos entonces que cuando hemos establecido enunciado cuantificado existencialmente, por complicado que sea, es decir, uno en el que el cuantificador existencial ∃ está fuera de cualquier paréntesis en el enunciado, ahora sabemos que hay algo en el dominio relevante de cuantificación que tiene las características relevantes. Por lo tanto, a partir de enunciados cuantificados existencialmente podemos inferir que existe algo en el dominio de cuantificación que tiene las características relevantes. Hay algún ‘x’ que puede sustituir al valor de esta variable que hace que el enunciado sea verdadero. Para el enunciado,
∃x (Px ∧ Exa),
el objeto que puede sustituir al valor de la variable para hacer que enunciado sea verdadero es (como acabamos de ver) Platón.
Antes de abandonar este punto, vale la pena señalar que no todos los enunciados que contienen cuantificadores existenciales nos permitirán inferir que existe algo que tiene ciertas características. En términos generales, incluso si un enunciado contiene un cuantificador existencial, si el cuantificador no está fuera de todos los paréntesis del enunciado, entonces uno no está autorizado a concluir que existe algo con las características relevantes. Por ejemplo, considere estos enunciados en lógica de primer orden:
Fa ⊃ ∃xPx (léase: Si ‘a’ es una ‘F’, entonces algo es una P.)
∃xPx ∨ ∃xQx (léase: O algo es una ‘P’ o algo es una ‘Q’.)
¬∃xPx (léase: No es el caso de que algo sea una ‘P’.)
Ninguna de estos enunciados implica la existencia de algo que sea una ‘P’. Puede darse cuenta de ello inmediatamente porque el cuantificador existencial no está fuera de todo el enunciado.
Por último, debemos destacar una diferencia entre los enunciados cuantificados universalmente y los cuantificados existencialmente. En general, la forma de pensar en la diferencia es que los enunciados cuantificados existencialmente te dicen que algo existe, mientras que los enunciados cuantificados universalmente (aquellos con un ‘∀’ fuera del paréntesis) dicen que todo es de cierta manera. Los enunciados cuantificados universalmente por sí solos no implican la existencia de nada. Entonces, por ejemplo, si ves una afirmación como «Todos los electrones tienen carga negativa», podemos escribirla en lógica de primer orden como:
∀(Ex ⊃ Nx).
Este enunciado por sí solo no implica que haya electrones. Solo dice que, si hay electrones, entonces tienen carga positiva. El siguiente enunciado implica la existencia de electrones:
∃xEx.
También lo hace:
∃x (Ex ∧ Nx),
que simboliza la afirmación de que existe al menos un electrón y que tiene carga negativa. Así pues, si buscamos afirmaciones que impliquen la existencia de algo en metafísica, nuestra atención debería dirigirse a aquellos enunciados que están cuantificados existencialmente, en oposición a aquellos que están cuantificados universalmente.
Los enunciados cuantificados universalmente tienen otros usos. Son especialmente útiles cuando se quieren enunciar principios universales. Algunos ejemplos de principios universales que se encuentran en los debates metafísicos son:
- Nominalismo: Todo es concreto. ∀xCx
- Idealismo: Todo es una idea en una mente. ∀xIx
- Presentismo: Sólo existen los objetos presentes. ∀x(¬Px ⊃ ¬∀y(x=y)
- Actualismo (en inglés Actualism de “actual”, : Todo es real (o todo existe realmente) ∀xRx
Una vez establecida una afirmación universal como esta, se puede utilizar la generalización universal (GU) para concluir sobre objetos particulares en el dominio de la cuantificación que tienen las características relevantes. Por ejemplo, los idealistas generalmente pretenden que su tesis sea integral, en otras palabras, una afirmación sobre la naturaleza de todo lo que existe. Esto implica que el dominio de cuantificación que es relevante para el idealista es el conjunto de todas las entidades que existen. Entonces, si uno es un idealista y, por lo tanto, cree que todo lo que existe (lo que sea) es una idea en una mente, entonces, utilizando la generalización universal, se puede concluir de:
∀xIx,
y el hecho de que (digamos) Taylor Swift existe:
∃x x=t (Existe algún x tal que x es idéntico a Taylor Swift),
Eso es:
It.
Esto puede leerse como: «Taylor Swift es una idea en una mente».

Note que al formular algunas de las afirmaciones de los últimos párrafos, hemos hecho uso del símbolo ‘=’ para representar la relación de identidad. La identidad es otra relación de dos posiciones, como la relación de admiración (simbolizada arriba con ‘Axy’). Es una relación que es de especial interés para los metafísicos y es particularmente útil para formular tesis metafísicas. Tendremos mucho más que decir sobre la identidad a partir de nuestros primeros pasos en discusiones relativas a la ontología.
¡Enhorabuena! Nos ha acompañado hasta aquí, le invitamos a resolver el Ejercicio 9.
Ir a la Siguiente Lección
Ir al Índice de Las Lecciones preliminares de Lógica
Ejercicio 8
Pēnsum VIII
Traducir enunciados a la lógica predicativa de primer orden
Usando las convenciones brindadas a continuación, traduzca las siguientes oraciones al lenguaje de la lógica de predicados de primer orden.
Clave:
a: Antonio
b: Bruno
Ix: ‘x’ es inteligente
Ex: ‘x’ es un estudiante
Px: ‘x’ es un profesor
Rxy: ‘x’ respeta a ‘y’
Enunciados:
- Antonio es un estudiante.
- Antonio es un estudiante inteligente.
- Alguien es un estudiante.
- Alguien es un estudiante inteligente.
- Antonio respeta a Bruno.
- Antonio respeta a alguien.
- Alguien respeta a Antonio.
- Algunos profesores respetan a algunos estudiantes.
- Todos son profesores.
- Todos los estudiantes son inteligentes.
¡Muy bien! Ahora puede continuar a la Parte II.
Tabla 3
Cuatro Reglas de la lógica predicativa
|
Introducción del cuantificador existencial (IE) A partir de cualquier cosa de la forma: Fa
Se puede inferir: ∃xFx |
Introducción del cuantificador universal (IU) Si se ha introducido un nuevo término ‘a’ como un nombre arbitrario, y se ha demostrado para él que: Fa Entonces se puede inferir: ∀xFx |
|
Generalización del cuantificador existencial (GE) Si se ha establecido que: ∃xFx Entonces se puede introducir un nuevo término ‘a’ en el lenguaje para referirse a cualquier objeto en el dominio de cuantificación que satisfaga la descripción ‘es F’ y concluir: Fa |
Generalización del cuantificador universal (GU) A partir de cualquier cosa de la forma ∀xFx
Se puede inferir utilizando cualquier nombre ‘a’ que se refiera a algo en el relevante dominio de cuantificación que: Fa |
Ejercicio 9
Pēnsum IX

Reconocimiento de formas válidas de argumentos en lógica predicativa
En los siguientes ejemplos, indique cuál de las cuatro formas válidas de argumentos representan los argumentos (IE, GE, IU o GU), o si la respuesta es «Ninguna de las anteriores».
- Todos somos mortales. Por lo tanto, Taylor Swift es mortal.
- Algunos humanos tienen libre albedrío. Por lo tanto, Taylor Swift tiene libre albedrío.
- Sócrates vivió en el pasado. Por lo tanto, existe algo que vivió en el pasado.
Ir a la Siguiente Lección
Ir al Índice de Las Lecciones preliminares de Lógica
Notas
- 1Recordemos que estamos ante unas lecciones preliminares que son propedéutica a un curso introductorio a la metafísica.
- 2Claro está que podríamos utilizar el método que aprendimos en la lección sobre Validez.
- 3A diferencia de «Marco es ordenado» y «Robert es un filósofo», en los que nos encontramos frente a predicados de una posición.
- 4En inglés: bound variable.
- 5En inglés: Domain of quantification.
- 6Que desafortunadamente aún no trataremos en estas lecciones preliminares de lógica. Contacte con nosotros para considerar su incorporación al Atrium Philosophicum. Show the love!
- 7emplearemos P de philosophī.
- 8Philosophus
ADEPTVRIS DOCTRINAM ***
ARS QVAERENDĪ ***
